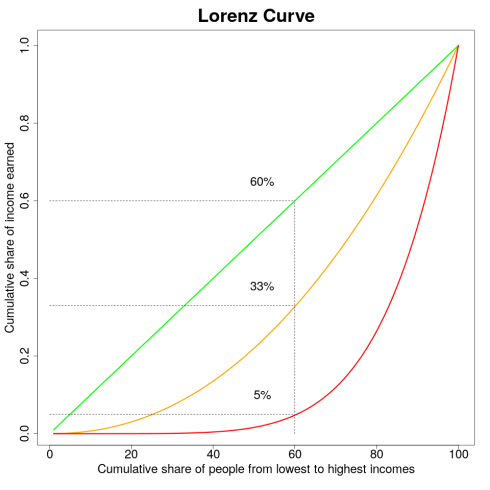
The Lorenz Curve displays the actual income or wealth distribution of an economy. The concept was brought up by the American economist Max O. Lorenz in 1905. The curve represents a graphical representation of the income or wealth distribution of an economy or country. That is, it shows the proportion of income earned or wealth possessed by any given percentage of the population. In the case that everyone has approximately the same wealth, we have a very equal society. While in a case where few own the majority of wealth, we have high inequality. The following figure depicts the Lorenz curve for three economies with varying degrees of inequality.

The green, 45-degree line shows the Lorenz Curve of an economy with a perfectly equal wealth distribution. The orange line shows an economy with an unequal wealth distribution and the rel line depicts a very unequal wealth distribution. Generally, the further away the Lorenz Curve from the diagonal, the more unequal the wealth distribution. The degree of inequality is often expressed in terms of the Gini Coefficient. The Gini Coefficient is equal to the area between the actual income distribution curve, as expressed by the Lorenz Curve, and the line of perfect income equality.

The Lorenz Curve represents the actual distribution of wealth in an economy and can be interpreted the following way: In an economy of perfect wealth equality (green line) the 60% of the population own 60% of the national wealth. While in a case of inequality (orange line), the poorest 60% of the population would own only 33% of the overall wealth. In the case of very strong inequality (red line) the the poorest 60% of the population own only 5% of total wealth. While the richest 40% own 95% of the wealth. The more bowed out a Lorenz Curve, the higher is the inequality of wealth in an economy.

The following post explains how to compute the Lorenz Curve. Besides the tutorial on how to compute the Lorenz Curve on your own, the post also provides an R code for easy replication.